You are given co-ordinates of the boundary of a farm. The information about the farm are as follows:
- Building a single shelter costs 25 units.
- The farm lies in an \(infinite 2D\) plane.
You are required to write a program to calculate cost for building maximum number of shelters at some integral point strictly inside the fencing.
Input format
- First line contains a single integer N denoting number of logs used for fencing.
- Next N line contains two space-separated integers X and Y denoting the X and Y co-ordinates of the logs.
- Points are given in a counterclockwise direction.
Output format
Print the cost to build the maximum number of shelters.
Constraints
\(3 \le N \le 2 \times 10^5\)
\(1 \le X, Y \le 2 \times 10^6\)
4 2 1 4 3 3 5 1 4
125
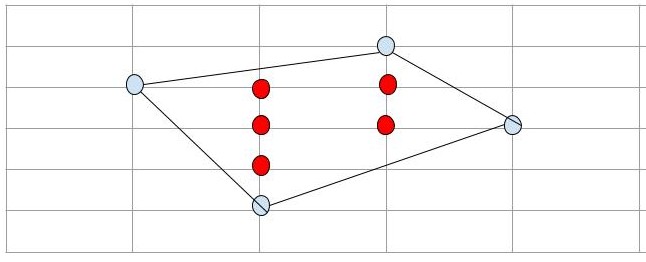
See the image for explanation. There are 5 points in the interior of fencing where they can create shelters. Red points denote the location of shelters.
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor
Login to unlock the editorial
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor