Let’s define a term “Powerful Pair” as pair of two integer numbers, say A and B such that bitwise xor of these integers ( say, A xor B ) is a power of 2.
You are given a tree rooted at vertex 1 and total N vertices where each node contains a value in it. You have to answer Q queries. In each query, you will be given two vertices U and V, your task is to count the number of pairs of vertices (X, Y) (not necessarily distinct) such that X belongs to the subtree rooted at U and Y belongs to the subtree rooted at V and values in these vertices form a Power Pair.
Input:
Input starts with an integer N (1<=N<=100000), denoting the total number of nodes in tree. Next line contain N space separated integers denoting the values in node starting from 1 to N, which is nonnegative integer having value at most 100000. Next N-1 line contain two space separated integers, denoting an edge in tree. Next line will contain a single integer Q (1<=Q<=100000), denoting total number of quires. Following Q lines will contain two integers U and V separated by space between them.
Output:
For each query, output an integer denoting total number of ways of forming powerful pairing in between the values of subtrees given in each query.
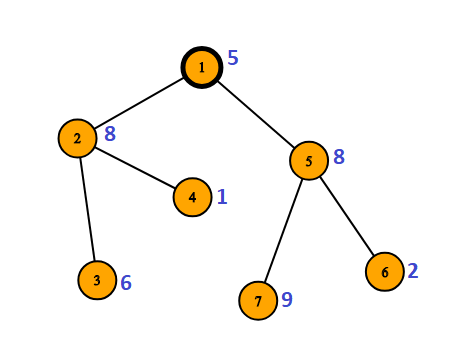
In sample 1, there ate 3 powerful pairing in between subtree rooted at 2 and 5 , which are :
( 2 , 7 )
( 4 , 7 )
( 3 , 6 )
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor
Login to unlock the editorial
Please login to use the editor
You need to be logged in to access the code editor
Loading...
Please wait while we load the editor